We just arrived at Ottawa at 6pm today, ready to attend CEEA 2019. I am impressed by the app Guidebook ( https://guidebook.com/ ) that the organizer chose to use. As long as the app is downloaded to my phone, I can see everything about the conference: speakers, sessions and talks, locations, and I can make my own timetable base on which talk(s) I plan to go. It’s very intuitive to use and such an environmentally friendly idea. I’ll come back to this post after tomorrow. Stay tuned!
First workshop: it’s interesting to hear what challenges people have regarding use of OER: it’s free for users, but how about developers? Who’s going to fund all these projects? Is it possible to find resources other than textbooks? How about projects, free softwares, workshop materials?
http://diy.open.ubc.ca/ and http://www.learncheme.com/ offer a variety of open-licensing materials; the latter focuses on chemical engineering, including videos, interactive simulations, and interactive self-study modules.
Afternoon sessions start with a workshop about active learning. I’m here because I want to know whether it’s possible to use this pedagogy in my large first-year calculus class, especially when I don’t have any TA’s help.
Part I Exploring active learning: flipped classroom; think-pair-share; co-operative learning; reflections; discussion questions; concept mapping; peer instruction. We need to think critically and reflectively about our teaching practice.
What is “active” in active learning? It’s about the level of engagement among learners, and whether learning and progress is happening. We were also given the chance to talk about challenges we face in my teaching, learning or mentorship: personally for me the main challenge is lack of interaction with colleagues, and lack of autonomy when it comes to course design. There seems to be little opportunity built-in the college system that actively promote interactions between course instructors. It could happen that a team of instructors teaching the same course never meet till the moment of final exam. I would love to get to know people better, to learn what people are doing for their teaching and to exchange ideas but I have yet to find an efficient way to achieve that goal. Right now almost all the conversations that happened are point-to-point. It’s challenging for someone new like me who just joined the department and who’s not on a continuous appointment stream. Another point that was brought up is when active learning was implemented through team-based work, there are always students who do not participate and engage in the activities. How to motivate them to be more engaging?
Part II Thinking about care and our role:
Part III Generation of new frames:
Frame 1: create environments and conditions that support learners to construct meaningful……
Frame 2: Think about content, instructional activities, and assessment- and the alignment of all three.
Frame 3: Be intentional about how the active learning exercise can support students in making meaning.
I’ve learned to ask questions about why we do what we do, and always try to learn students’ perspective in their learning journey.
I’m back home from this exciting event and I’m so glad that I made it. The best part of it is all the conversations that I was part of and all the connections that happened in-between talks. People are so generous sharing their own teaching practices with me, including their favorite books for active learning in large classes! Even though I was surrounded by engineers and engineering educators, we have a lot in common when it comes to teaching. Look forward to CEEA2020!
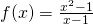 and
and 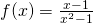 , and visualize removable discontinuity, vertical asymptote and horizontal asymptote.
, and visualize removable discontinuity, vertical asymptote and horizontal asymptote.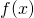 and which one is
and which one is 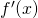 .
.