Dear students from MAT223:
I’ve received some requests to explain the following questions and I made a few short videos to explain how to solve them.
Happy learning!
- If
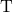 and
and 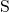 are linear transformations
are linear transformations 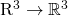 , and
, and 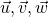 are three distinct vectors in
are three distinct vectors in 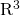 so that
so that
![]()
then ![]() for all
for all ![]()
2. If A is ![]() matrix and dim(null(A-I))=3, then A is diagonalizable.
matrix and dim(null(A-I))=3, then A is diagonalizable.
3. Consider
![Rendered by QuickLaTeX.com \begin{equation*}A=\left[ \begin{array}{rrr}2 & 4 & -1 \\0 & 7 & 2 \\0 & -2 & 3\end{array} \right]\end{equation*}](https://mathrojak.ca/wp-content/ql-cache/quicklatex.com-c17f811705028b3063dba6288b419b46_l3.png)
Decide whether A is diagonalizable. Justify your answer.
4. What is the matrix of a linear transformation
![]()
with
![]()
Compute the rank of this matrix.